Computer Science
Trees
What Is A Tree?
A tree is a dynamic data structure in which data is stored in a hierarchical manner.
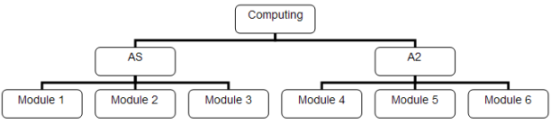
In the above diagram, each part of the tree that contains information (the boxes) is called a node. The first node (in this diagram - 'Computing') is called the root node. The lines which connect each of the boxes are called branches. Some nodes have child nodes - they connect to nodes on the level below. Nodes that don't have children are called leaf nodes.
A tree is very similar to a graph. In fact, we could say that the tree shown above is a connected, undirected graph. This particular tree is a rooted tree. All of the edges are directed away from the root node.
Binary Trees
A binary tree is a special type of tree where each node is allowed a maximum of 2 children. You construct a binary tree by placing the first data item as the root node. For each subsequent item, branch to the left if it is less than the root node, branch to the right if it is greater. Apply this branching rule at each node that is met unitl the item can be placed.
Do this with the following names,
Partridge, Duckworth, Smith, Arkwright, Wren, Thumbface, McJack.
You should end up with a tree diagram that looks like this,
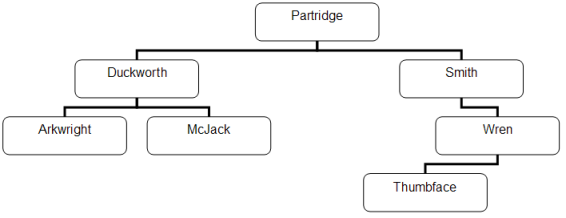
Starting from the root node, if you were searching for Thumbface, which items would you need to access?
Make another tree with the following captial cities,
London, Paris, Washington, Canberra, Lima, Madrid, Lisbon.
Which data items would be accessed if you were searching for Madrid?
Traversing The Tree
There are a variety of methods used for traversing the tree to produce sorted output. The following traversal methods produce output in different orders.
- Pre-Order Traversal
- In-Order Traversal
- Post-Order Traversal
A diagrammatic representation of how to construct a binary search tree, as well as the different traversal methods, can be found by clicking or downloading the following PowerPoint slideshow. DOWNLOAD BINARY TREE SIMULATION
Javascript Binary Tree Simulation
Remember that the diagrams shown in the slideshow are simply a way of representing the structure of the tree. In order to program with the tree, there is no need to replicate the visuals. In the example below an array of records is used. Each record has 3 properties, a name, a left pointer and a right pointer. The pointers indicate the address of the left or right child of a node. Add some names and watch how the pointers change as each item is added. Then press the buttons and see how they are sorted.
Binary Tree Algorithms
The simulation on this page uses an array of records to manage the items in the binary tree. The structure definition is shown in C#, the remaining algorithms are pseudocode.
Record Definition & Global Variables
public struct TreeItem {
public int left;
public int right;
public string name;
}
int maxsize = 15;
TreeItem[] treeitems = new TreeItem[maxsize];
Inserting Items In The Tree
Two procedures are used. The first checks that the tree is full and, if not then looks to see if this is the first item (root node) of the tree. If this is the root node it creates it, no fuss involved since the root node initially points to 0. If the node is not the root, the second procedure is called. This procedure is recursive, walking through the tree following the left/right rules changing the appropriate pointer of the parent node.
Procedure InsertItem(itm)
IF treeitems.length = maxsize THEN Exit Procedure
IF treeitems.length = 0 THEN
treeitems[0] = new TreeItem(itm)
ELSE
treeitems[treeitems.length] = new TreeItem(itm)
ChangePointers(treeitems.length - 1, 0)
END IF
End Procedure
Procedure ChangePointers(a,b)
IF treeitems[a].name < treeitems[b].name THEN
IF treeitems[b].left = 0 THEN
treeitems[b].left = a
ELSE
ChangePointers(a, treeitems[b].left)
END IF
ELSE
IF treeitems[b].right = 0 THEN
treeitems[b].right = a
ELSE
ChangePointers(a, treeitems[b].right)
END IF
END IF
End Procedure
In-Order Traversal
The procedure for in-order traversal is recursive. The first call to this procedure would be InOrderPrint(0).
Procedure InOrderPrint(a)
IF treeitems[a].left <> 0 THEN
InOrderPrint(treeitems[a].left)
END IF
Print treeitems[a].name
IF treeitems[a].right <> 0 THEN
InOrderPrint(treeitems[a].right)
END IF
End Procedure
Pre-Order Traversal
Procedure PreOrderPrint(a)
Print treeitems[a].name
IF treeitems[a].left <> 0 THEN
PreOrderPrint(treeitems[a].left)
END IF
IF treeitems[a].right <> 0 THEN
PreOrderPrint(treeitems[a].right)
END IF
End Procedure
Post-Order Traversal
Procedure PostOrderPrint(a)
IF treeitems[a].left <> 0 THEN
PostOrderPrint(treeitems[a].left)
END IF
IF treeitems[a].right <> 0 THEN
PostOrderPrint(treeitems[a].right)
END IF
Print treeitems[a].name
End Procedure

