Computer Science
Data Representation
Program Design
Hardware & Software
Networks
Databases
Data Structures
Algorithms
Other
Computer Science
Finite State Machines
Introduction
Remind yourself of the material covered in the Comp1,
State Transition Diagram
The following is a generic state transition diagram.
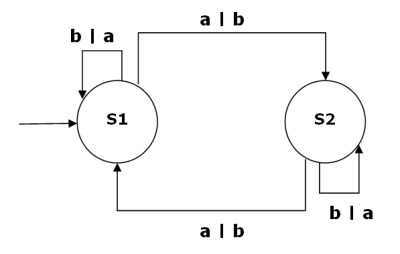
The circles labelled S1 and S2 represent the states of our machine. The arrows between the states (which might be represented with arcs) are called transitions. The transitions are labelled with two symbols (a | b) where a is the input symbol or the trigger for the transition. The second symbol (b) is the output symbol. The starting state is indicate with an arrow on the left of the diagram.
This FSM, has two possible input symbols. It can therefore be said to have an input alphabet of {a, b}. Since the same two symbols are used for output in this FSM, its output alphabet can be said to be {a,b} as well.
The output symbol can also be replaced with an action if the machine is to do this instead of output a symbol.
If there is only one possible next state for each pair of current state and input symbol, the FSM is said to be deterministic. If, in our diagram, the input of a in S1 could trigger a change to S2 or back to S1, the FSM would be said to be non-deterministic.
State Transition Table
A state transition table can be used to represent the transition function of an FSM.
| Current State | S1 | S1 | S2 | S2 |
| Input Symbol | a | b | a | b |
| Next State | S2 | S1 | S2 | S1 |
| Output Symbol | b | a | b | a |
Types Of Finite State Machine
Finite State Machines which produce output can be either Moore Machines or Mealy Machines.
Moore Machine
In a Moore machine, the transitions are labelled with inputs only. The outputs are labelled with the states. The following FSM is a simple example of a Moore machine.
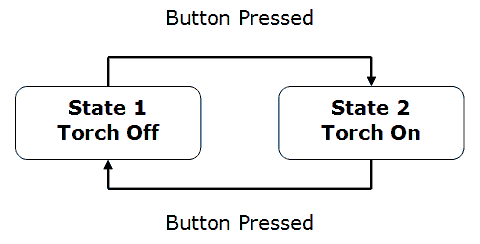
Since the state of a Moore machine depends on the sequence of inputs that it has received, there is a sort of memory for this. The example is a bit limited but, suppose we labelled State 1 as our starting state. We can see that, if the current state of the FSM is State 2, there have been an odd number of button presses. For State 1, either 0 or an even number of button presses.
Mealy Machine
A Mealy machine has the outputs associated with the transitions. This means that transitions depend on the current state and the input value. In a Moore machine, the output would depend on the state you transition into, not the input you used to do so. With a Mealy machine, it is the input and previous state that determine the output.
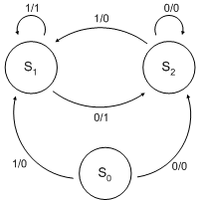
There is an equivalent Moore machine for each Mealy machine. The names of these machines are, as you would hope, derived from their proposers - Mr Moore & Mr Mealy.
Finite State Automata
A Finite State Automaton or FSA, is a finite state machine for which there are no outputs.
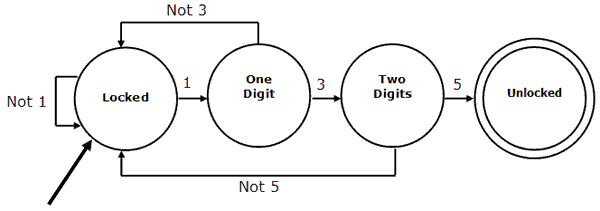
The arrow pointing into the locked state indicates the initial state. The double circle for the unlocked state indicates the goal or accepting state. FSAs are used to solve decision problems. In the example, there is only one accepting state - the machine continues until the correct sequence of input has occurred. We can read the unlocked state as being an output of YES for our decision problem and all other states as an output of NO.
FSAs may be deterministic (only one output exists for each state/input pair) or non-deterministic (the same state/input pair can produce different transitions). One important aspect of the two is that for every non-deterministic FSA, there is an equivalent deterministic FSA that accept the same input alphabet. There may need to be (a lot) more states in order to implement the FSA, but it can be done. This equivalence is important since a non-deterministic FSA is likely to be easier to construct. Some problems are easier to model with an NFSA than with A DFSA.