Computer Science
Recursion
A procedure is recursive if the procedure contains a call to itself. This is perfectly legitimate in C# and most other high-level languages. A characteristic of recursive procedures is that there must be a stopping condition that can always be reached by the procedure.
The following procedure will calculate the factorial of a number (3! = 3 x 2 x 1 = 6) using a recursive technique.
static int RecursiveFactorial(int num)
{
if (num == 1)
{
return 1;
}
else
{
return num * RecursiveFactorial(num - 1);
}
}
There is an obvious danger with recursion. In a more complex function, you really need to make sure that there is always stopping condition.
The need to use a stack to store return values means that recursive techniques can be heavy on the memory use. A stack is only so big and a stack overflow would cause the program to crash.
Non-recursive solutions are therefore likely to be more efficient when it comes to processing time and storage. However, there are still reasons why recursion is a desirable feature in a programming language. In some cases, the code is easier to write and understand for the programmer than an iterative solution. This, in some cases, is more important than performance.
Dry-Running Recursive Procedures
You may be asked to dry-run a recursive procedure during the examination. This is slightly more complicated than for an iterative procedure - you need to keep track of the procedure calls.
Example
Dry-run the following procedure using the table of data shown below. The program starts with Process(1).
Procedure Process (P)
Print (P)
If Table[P].Left <> 0
Then Process (Table[P].Left)
EndIf
Print (Table[P].Data)
If Table[P].Right <> 0
Then Process (Table[P].Right)
EndIf
EndProcedure
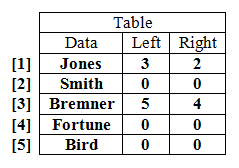
- Label the program with line numbers - it will help you keep track of where you are within the program.
- Make sure that you understand the way that the elements in the table are referenced.
- Find rough space to create a table to store the information that would go into a stack each time the procedure calls itself. Fill the stack from the bottom - it is LIFO.
- Create a space to write out the printed output each time a Print statement is executed.
Fibonacci Numbers - The Revenge Of Recursion
Fibonacci numbers can be calculated using either recursive or iterative routines.
Fibonacci - Recursive
function fib1(n)
if n = 0: return 0
if n = 1: return 1
return fib1(n - 1) + fib1(n - 2)
End Function
Fibonacci - Iterative
function fib2(n)
if n = 0: return 0
if n = 1: return 1
create an array f[0 � n]
f[0] = 0, f[1] = 1
for i = 2 � n:
f[i] = f[i -1] + f[i - 2]
return f[n]
End Function
As the input value of n increases by 1, the iterative algorithm requires 1 additional step (the for loop runs once more). The same is not true of the recursive algorithm.
If we were to call the recursive procedure with n=5, the following calls would be made to this procedure.
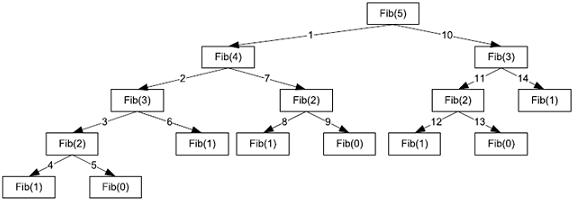
As n increases, the number of function calls quickly gets out of hand. If you look at the following table, you can see that by around n=10, the number of function calls is already very high. By n=20, the number of function calls is over 20000.
| n | Recursive Calls |
|---|---|
| 2 | 2 |
| 3 | 4 |
| 4 | 8 |
| 5 | 14 |
| 6 | 24 |
| 7 | 40 |
| 8 | 66 |
| 9 | 108 |
| 10 | 176 |
If you implement both algorithms in C# and use the System.Diagnostics tools, you can compare the execution time of both algorithms. The recursive procedure will crash the computer long before the iterative procedure. The main limit on the use of the iterative procedure is the size of number you can store using built-in data types.

