Visual C# (Windows) Guide
Sudoku: The Future
Tidying Up The Application
Before moving on, you should consolidate the work done so far. There are some bits of validation that could be included within the program to make it more robust and less likely to crash. You might also notice that, if you use the solving procedures and then open a new puzzle, the output box is not cleared. You should be able to sort this out quite easily
Checking For A Solved Puzzle
An obvious omission from these pages is a method to check whether a puzzle is solved. This method will need to be called every time the SolveNextStep() method is called as well as after each operation (a user entering a value or one of the solving methods being successful). A nice 'tada' sound would be good as well as some sort of congratulatory message.
Bear in mind that a puzzle can be considered to be solved if each row, column and minisquare contains the numbers 1-9 only once for each number. One approach would be to start with a string with the value "123456789". Examine the value of the first cell in a row and use the string.Replace() method to replace that value in the string with an empty string "". Continue this process with the remaining cells in the row. At the end of the row, your string should be empty. If it is not, the puzzle is not solved. Repeat this process across each row, cell and minisquare to check the entire puzzle.
An alternative approach is to use an array rather like our array of candidates. We can set each value to 1 when it is found in a group. There should be no zero values left in the array when the whole group is examined.
User Candidate Elimination
Currently, the application takes care of all candidate elimination. A truly useful application would allow a user to do that themselves when they are solving a puzzle without using the solving functions.
This feature could be added to the context menu strip and is very easy to test.
Undo Feature
This is quite tricky to do. Each move can result in entering a value or eliminating a series of values. In order to 'undo' an operation, the application needs to keep track of the operations it performs and have methods to allow it to rollback. The feature would be very useful to the user.
Highlighting
A useful feature of the application might be to highlight all cells containing a particular candidate value. It may be easy to see where a particular value should be placed when you have temporarily 'filtered out' the other candidates.
Solving: Naked Triples / Triplets
The best way to move the application on is to add solving methods. The more methods we have, the greater the chance that any puzzle can be solved by our program. Naked Triples is a similar strategy to the Naked Pairs strategy we examined on the previous page except that it involves 3 values. Study the screenshot,

The red dots on the cells in this row form a naked triple. The numbers 1, 8 & 9 must be contained within these 3 cells in this row and can be eliminated from any of the cells. Notice that triples will be harder to spot than pairs - not all of the cells have to contain all of the values.
Another issue with naked triples is that, as more values are entered into the puzzle, it is less likely that the candidates that form the triple appear in other cells in the row, column or minisquare.
The same logic can be used with quadruples - groups of 4 candidates that are shared between 4 cells. Again, spotting the quadruple that allows some elimination is the key.
Solving: Locked Candidates
This a very powerful solving strategy that can be quite hard to spot in the puzzle. Look carefully at the screenshot in which all the cells which have 5 as a candidate are marked with a red dot.
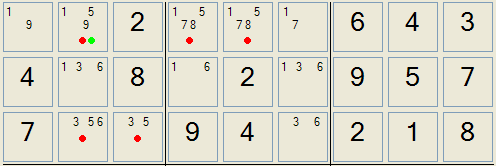
The rules of sudoku dictate that there must be a 5 in each row. Looking at our candidates, the 5 on row 3 can only be in the left hand minisquare. We can therefore eliminate 5 as a candidate from the cell containing the green dot. If you look carefully, you will see that this is a move that 'unlocks' quite a few other operations on the puzzle shown.
Solving: Hidden Pairs

When two candidates appear only in two cells of a group (row, column or minisquare), all other candidates can be eliminated from those cells. In the screenshot, the cells marked red are the only cells in the column which contain the candidates 4 & 9. These cells must therefore be either 4 or 9 - all other candidates can be safely eliminated from those cells.
Like many of the solving strategies, the same principle can be applied to cells in rows and minisquares where 2 candidates appear only in 2 cells.
You can also have hidden triples and quads although they are less likely to be found in a puzzle by our application since it always tries out the easy methods first.
Solving: More Methods
There are a few more strategies that can be used to solve a puzzle. Notice that all of our methods have been based on logic - there is no testing out and backtracking in our program. You will have to do a bit of research on these if you want to extend your program further.
Solving: Brute Force
Truly difficult puzzles may exhaust all of the solving strategies that you have programmed. In that case, you would have to resort to a brute force approach. This involves testing all possible avenues until one is found.
At the point that you begin to use this strategy, you would need to store the state of the puzzle. Locate a cell with as few candidates as possible (preferably just 2). Randomly pick a value for that cell and see if the puzzle can be solved. If the program cannot solve the next step at any point, try the other or one of the other candidates. Eventually, a solution will be found.

