Visual C# (Windows) Guide
Sudoku: Advanced Solving
The program can only solve the simplest puzzles so far. To solve the average puzzle from a newspaper, we need to add a few more solving methods.
Solving: Naked Pairs/Twins
One powerful strategy for solving puzzles is to look for what we can call twins or naked pairs. Study the screenshot below,
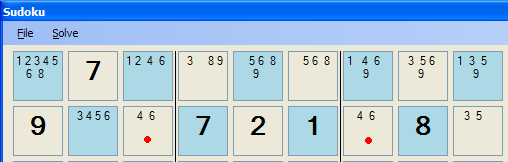
Look carefully at the two cells with the red dot. These cells have two candidates, 4 and 6. Logic dictates that one of these cells must be 4 and the other 6. We don't know which one at this stage but that doesn't matter. What we do know is that these two numbers cannot appear in any other cell in the row. That means we can eliminate them as candidates from all other cells in the row. We may then find another step that can be solved more easily.
Naked pairs can occur in rows, columns or minisquares. To find them in say, a row, we have to find two cells in the row that have only two candidates and where the candidates are identical. We already have two methods in the GridSquare class that can help with this - NumCandiates() and DisplayCandidates().
Solving: Naked Pairs In Rows
To find naked pairs in rows we need to,
- Start with the first row
- Look at each cell and check if there are exactly two candidates
- Check the remainder of the row for a cell with the same 2 candidates
- Loop throught the other cells in the row and eliminate the 2 candidates from all cells except the pairs
- If there were eliminations return a message and stop looking
- If not, continue looking for pairs in this row, moving onto the next if none are found.
The method to do this in our program is shown below. It is a bit of a beast and needs reading carefully to make sure that you can see what is happening.
public string FindNakedPairInRow()
{
string returnMessage = "0";
for (int row = 1; row <= 9; row++)
{
for (int col = 1; col <= 9; col++)
{
if (GridCell[row, col].Value == 0 && GridCell[row, col].NumCandidates() == 2)
{
//cell has two candidates - check for a match in the remainder of the row
for (int checkCol = col + 1; checkCol <= 9; checkCol++)
{
if (GridCell[row, checkCol].Value == 0 && GridCell[row, checkCol].DisplayCandidates() == GridCell[row, col].DisplayCandidates())
{
//naked pair found - what are the values
string numString = GridCell[row, checkCol].DisplayCandidates();
numString = numString.Replace(" ", "");
int numToEnter = System.Convert.ToInt32(numString);
int val1 = numToEnter % 10;
int val2 = (numToEnter - val1) / 10;
//now eliminate these values from other cells in the row
bool changeMade = false;
for (int i = 1; i <= 9; i++)
{
if (i != col && i != checkCol)
{
if (GridCell[row, i].Value == 0 && GridCell[row, i][val1] == 0)
{
GridCell[row, i][val1] = 1;
changeMade = true;
}
if (GridCell[row, i].Value == 0 && GridCell[row, i][val2] == 0)
{
GridCell[row, i][val2] = 1;
changeMade = true;
}
}
}
if (changeMade)
{
//found naked pair - values have been eliminated
returnMessage = "Row " + row + ": Naked Pairs " + numString + " in " + row + "," + col + " and " + row + "," + checkCol;
return returnMessage;
}
}
}
}
}
}
return returnMessage;
}
Obviously, you plug this method into the SolveNextStep() method as you have with the others
Solving: Naked Pairs In Columns & MiniSquares
The FindNakedPairsInRow() method can be converted to work with columns. Look at how we changed the FindSingleInstanceInRow() method to work for columns on the previous page.
Remember that it is always a bit trickier to work with minigrids - but you should get there if you adjust the bullet point steps shown above to examine the values in a minigrid rather than a row or column.
Complete all 3 of the Naked Pairs methods and test the application before moving on.

