Visual C# (Windows) Guide
Fractals: Basic Application
It will help you greatly to have read the explanations on the previous few pages. On this page you will find the instructions for making an application that plots the image of the Mandelbrot Set that you saw on the previous page. Subsequent pages cover the development of a feature to allow the user to zoom in on various sections of the original image and how to colour the images.
The basic application looks like the screenshot below,
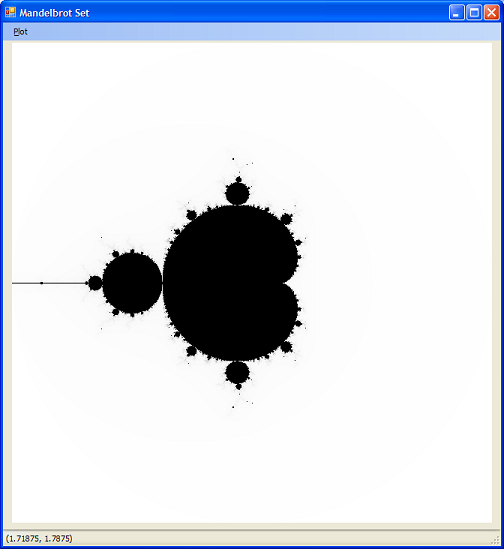
The fractal image will be drawn in a picture box called picMandel. The picture box is 640 x 640 pixels in size and its location is 12, 27. The form was named frmMandelbrot. A StatusStrip called statusStrip1 was added to the bottom of the form. It has a ProgrssBar and a StatusLabel added to the strip - you do this on the strip itself at the bottom of the form. Lastly, there is a MenuStrip at the top of the form.
Start by creating a new Windows Application project and setting up the controls with the names given above.
The status strip will show a progress bar as the image is being drawn. The label will be used to show the value of c at any point on the graph.
The menu is not really required at this stage but will be useful as you add all sorts of extras to the application later on.
Global Variables
The following global variables are needed and are placed at the top of the form's code window,
Bitmap bmpMandel = new Bitmap(640,640);
double unitsPerPixel = 0.0;
double minA = -2.0;
double maxA = 2.0;
double minB = -2.0;
double maxB = 2.0;
int maxIterations = 500;
The bitmap will be used to make the image. The unitsPerPixel will be calculated each time an image is drawn and will be used to convert pixel values to the values of c we are plotting. minA, maxA, minB, maxB represent the range of values of the real part of the complex number c (minA, maxA) and the range of the imaginary part of c (minB, maxB). Finally, maxIterations determines how many times we iterate the Mandelbrot algorithm before deciding whether or not a value of c is in the set. Changing this number will have an effect on the way the image looks.
Mandelbrot Function
This baby is what it's all about. The function has 3 parameters, a, b and maxit. The first 2 parameters represent the real and imaginary coefficients for the complex number c. The last parameter is the maximum number of iterations allowed.
public int IsInMandelbrotSet(double a, double b, int maxit)
{
double squareOfDistance;
double aSquare = 0.0;
double bSquare = 0.0;
double startA = a;
double startB = b;
int numIterations = 0;
while (numIterations < maxit)
{
aSquare = a * a;
bSquare = b * b;
squareOfDistance = aSquare + bSquare;
if (squareOfDistance > 4)
{
return numIterations;
}
b = 2 * a * b + startB;
a = (aSquare - bSquare) + startA;
numIterations++;
}
return numIterations;
}
The variable squareOfDistance will be used to keep track of the distance of the complex number z from the origin (0,0) on each iteration. If you look back at the diagram on the Complex Numbers page, you will see that you can make a triangle between the points (0,0), (x,y) and (x,0). The distance from (0,0) to (x,y) is the square root of the sum of the squares of the other two sides. In our program we won't actually take the square root of the value - the program runs quicker if we just check that it is less than 4.
So, what is happening here. We are using an initial value of z equal to 0, so the result of the first iteration of z2 + c is going to be c. We check that this value isn't already too large by working out the square of the real and imaginary parts (a and b). If this number is greater than 4, we return the number of iterations. If not we use these new values to make the complex number z for the first iteration.
After the if statement, the next two lines are performing the operation, z → z2 + c. A few explanations might help here. Firstly, multiplying a complex number a + bi by itself results in the following,
(a + bi)(a + bi)
a(a + bi) + bi(a + bi)
a2 + abi + abi + b2i2
a2 + 2abi + b2i2
Since i2 = -1,
a2 + 2abi - b2
If we separate into real and imaginary parts we get,
Real: a2 - b2
Imaginary: 2ab
That covers the z2 part. We add on startA to the real part since that is the real part of the complex number c. startB is imaginary part of the complex number c and is added to the new value of b.
Creating The Image
This procedure generates the image.
public void CreateMandelbrotImage()
{
bmpMandel = new Bitmap(640, 640);
unitsPerPixel = (maxA - minA) / bmpMandel.Width;
int numIterations = 0;
Color pixelC = new Color();
int grey = 0;
Graphics g = Graphics.FromImage(bmpMandel);
g.Clear(Color.White);
g.Dispose();
Cursor = Cursors.WaitCursor;
toolStripProgressBar1.Visible = true;
toolStripProgressBar1.Maximum = bmpMandel.Height;
for (int y = 0; y < bmpMandel.Height; y++)
{
for (int x = 0; x < bmpMandel.Width; x++)
{
double a = minA + (x * unitsPerPixel);
double b = maxB - (y * unitsPerPixel);
numIterations = IsInMandelbrotSet(a, b, maxIterations);
if (numIterations == maxIterations)
{
// is in set - colour black
bmpMandel.SetPixel(x, y, Color.Black);
}
else
{
//not in set - colour greyscale
grey = (int)(255 * ((double)(maxIterations - numIterations) / (double)maxIterations));
pixelC = Color.FromArgb(255, grey, grey, grey);
bmpMandel.SetPixel(x, y, pixelC);
}
}
toolStripProgressBar1.Value = y;
if ((y % 20) == 0)
{
picMandel.Image = bmpMandel;
Application.DoEvents();
}
}
picMandel.Image = bmpMandel;
toolStripProgressBar1.Visible = false;
Cursor = Cursors.Default;
}
The first 11 lines are used to get ready to draw the image. The bitmap is cleared, the scale is calculated, the cursor changed, and the progress bar set up.
We loop through each pixel in the picture box working through a row at a time. We use the unitsPerPixel value to convert the pixel to values of c that we want to plot. We check if the number is in the Mandelbrot set and colour it black if it is. If it is not, we colour it a shade of grey according to the number of iterations that it took before the distance got too large (more iterations = darker grey).
Every 20 rows we update the image. This shows the user what is happening. The statement Application.DoEvents() allows the program to refresh the picture box before performing the next iteration.
At the very end we make the picture box have the image we have just created and tidy up a little.
You can test the program at this stage. Add a click event handler for the a menu item, Plot. Add a call to this procedure there - CreateMandelbrotImage();
Displaying c In The StatusStrip
A little information that will come in useful when trying to make pretty pictures is to know the values of c you are working with. This allows us to 'zoom' in on various sections of the image to find the interesting stuff.
We will put this information into the label that we created on the statusstrip. The label will show the value of c for the point where the mouse is.
private void picMandel_MouseMove(object sender, MouseEventArgs e)
{
string a = System.Convert.ToString((e.X * unitsPerPixel) + minA);
string b = System.Convert.ToString(((bmpMandel.Height - e.Y) * unitsPerPixel) + minB);
string coords = "(" + a + ", " + b + ")";
toolStripStatusLabel1.Text = coords;
}
Notice that we use the unitsPerPixel variable to report the value of c that was used.
Having A Play
You can make this application zoom in by changing the values we gave to minA, maxA, minB, maxB. Be careful, this program is based on a square image. The same scale is used to convert pixels to values on both x and y axis. You can mess about with these values as long as the following is true of the numbers you choose,
maxA - minA = maxB - minB
Try substituting the following values into the global variable declarations,
double minA = -0.4;
double maxA = -0.3;
double minB = 0.6;
double maxB = 0.7; 
