Python For GCSE
A: Starting Off
B: Selection
C: Iteration
D: Lists
E: String Handling
F: Subroutines
G: File Handling
H: Turtle Graphics
I: Bonus Material
Python For GCSE
Quadratic Equations
Introduction
x2 - x - 6
In Maths, you might normally solve this by factorising.
(x+2)(x-3)=0
This would give you the following solutions,
x=-2,x=3
Look at the graph we get when we plot the function, y = x2 - x - 6,
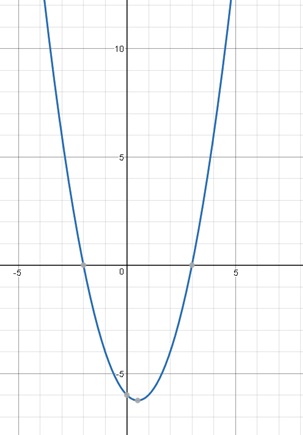
The shape of the graph is called a parabola. If the coefficient of x2 is negative, the parabola would be inverted. This parabola intercepts the x axis (y=0) at two points, the two solutions to the equation.
x2 + 2x + 1
(x + 1)(x + 1)
You only get a single solution, x=-1
When we draw the graph, this time the curve touches the x axis at its lowest point (highest point if the parabola is inverted).
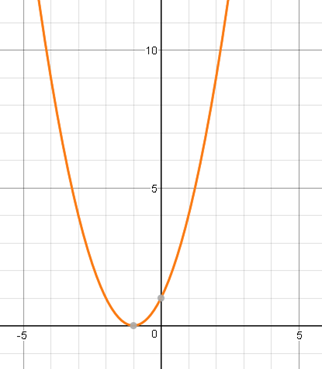
When we write a program to solve quadratic equations, we will need to deal with the fact that some quadratic equations only have a single solution.
x2 + x + 1
This equation cannot be factorised. There is no way that the -1 and 1 can be added or subtracted to make a total of 1.
Looking at the graph, we can see that the parabola does not intercept the x axis. We can’t solve the equation.
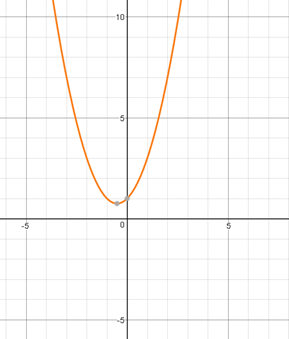
Our program is going to have to be able to cope with this third type of equation too.
The Quadratic Formula
Given a quadratic equation expressed in the form,
ax2 + bx + c
The solutions can be directly calculated with the formula,
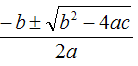
The following shows how we use the formula for our three types of equation,
Programming
The part of the formula that matters most is b2 - 4ac. This is known as the discriminant of the equation.
Our program needs to do something like the following,
d = b * b - 4 * a * c
IF d < 0 THEN
OUTPUT "Cannot Solve"
ELSE IF d == 0 THEN
x = -b / (2 * a)
OUTPUT "x = " + x
ELSE
rootd = square root of d
x1 = (-b + rootd)/(2 * a)
x1 = (-b - rootd)/(2 * a)
OUTPUT "x = " + x1 + ", x = " + x2
END IF
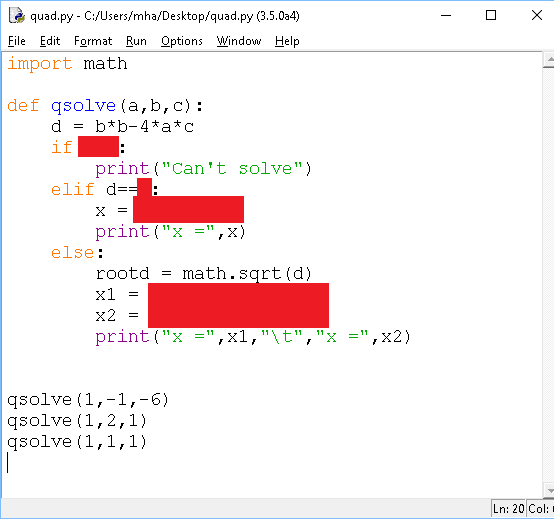
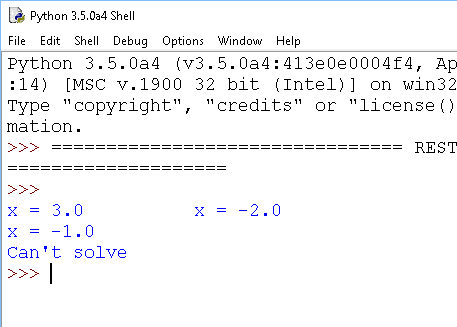
And here is an outline in Python with some strategic splodges,
