Python For GCSE
Bitwise Operators
Introduction
The screenshot shows the bitwise operators in Python. The are called 'bitwise' because they operate on the numbers at the level of the bit. That means that they are using the binary representation of the number when they perform the operation.
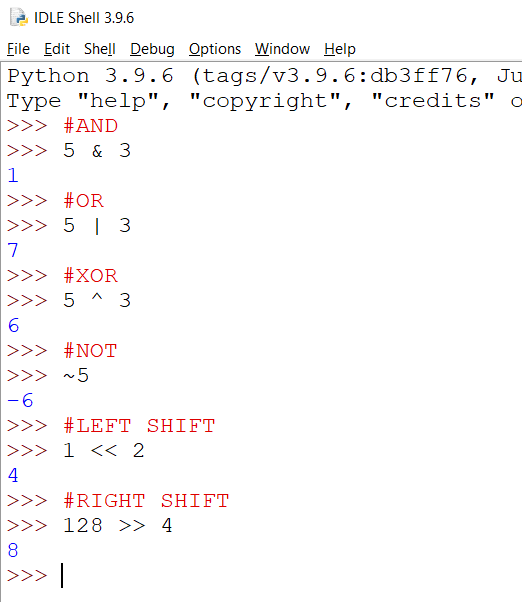
Let's work through each one of these to see if we can make sense of how we are getting the results that we are.
5 AND 3
The AND operator is the ampersand (&). To see how it is working, we line up the binary representations of each number, one above the other. Then we perform a logic AND operation with each column. The result is a 1 if the column contains two 1s, otherwise we get a zero.
101
011
001
That's how we end up with a result of 1.
5 OR 3
The OR operator is the pipe character (|). Again, we line up the numbers and do the logical OR operation on each column. The result is a 1 if either or both of the two numbers in the column are 1s.
101
011
111
5 XOR 3
The XOR operation is based on a logic gate that is not a part of the GCSE specification. It means 'exclusive OR'. It works in a similar way to the OR function except that two inputs of a 1 give the result of a zero. You can summarise an XOR by saying that it needs one or other of the inputs to be a 1, but not both. The symbol for this operator is the circumflex (^).
101
011
110
NOT 5
The NOT operator is a tilde (~). It flips the bits. When using this, you end up flipping the sign (positive or negative) of the number. You can read up about how the Two's Complement way of representing negative binary integers works to understand this more.
101 flip all bits, make the number negative and set the leftmost bit to 1
110
Left & Right Shifts
The left and right shift operators move all of the bits of a number a specified number of places to the left or right. A left shift of 1 is the equivalent of multiplying a number by 2. A right shift of 2 would divide a number by 2. When we are using binary integers, right shifts can mean that some place values are lost when they are moved right of the units bit.
1 << 2
001 becomes 100.
128 >> 4
10000000 becomes 1000.
Some Observations
AND
If we do an AND between a number and 1, the result depends on the number we start with. This is useful for reading bits in a number.
If we do an AND between a number and 0, we ignore the bits in the number we start with. This is useful for masking bits.
For example, take an 8 bit number.
10101001
00001111
00001001
If we do, number & 15, we can extract the digits from the first nibble. We mask (ignore) the other bits.
OR
OR is useful for turning on specific bits. If we do an OR with 1, we make a bit equal to 1, no matter what it was,
1001
1111
1111
XOR
XOR is useful for flipping bits. If we do and XOR with 1, we would transform the original bit of 0 to 1 and one of 1 to 0.
Tasks
These are quite challenging and they are meant to be. The idea behind these tasks is to build up a series of useful functions that you can use when you find the need for one of them in a program you are writing. Follow the guidance for each of the tasks and restrict yourself to using references for Python statements rather than looking for someone's answer.
Many of these can be achieved with only a few lines, some with just a return statement.
Task 1 - bitlength(n)
Get the number of bits in a number. Find the base 2 logarithm of n+1. Round it up using ceil. Both of these methods are in the math module.
Task 2 - parity(n)
Do an AND with 1. If the rightmost bit is a 1, the number is odd, otherwise even.
Task 3 - isbiton(n,p)
The idea for this one is to find out if the bit at position p in the number n is set to 1 or not. It should return True or False. To find out if the bit at place p is on, do an AND between n and a 1 which has been left shifted p places.
Task 4 - togglebit(n,p)
To toggle the bit at place p, do an XOR between n and a 1 which has been left shifted p places.
Task 5 - setbit(n,p,v)
You are setting the bit at place p to 1 if v is True, to 0 if it is False.
If you are turning the bit on, do an OR with a 1 which has been left shifted p times.
To turn a bit off, we can use masking. Left shift a 1 into the position you want to turn off (p places to the left), then invert the pattern with NOT to create the mask you need. Use an AND between n and your mask to get the result you need.
Task 6 - getbitslsb(n)
This function is meant to give you a list of the bits of a number, starting with the units bit. That is called the least significant bit (LSB). Make an empty list. Make a for loop repeat as many times as there are bits in n. In the loop, do an AND with 1 and append the value, then right shift the number a place before the next iteration.
You can also do this with a list comprehension for extra cool points.
Task 7 - getbitsmsb(n)
Copy your code from before. Define the list with something like bits = [0]*length, where length is the number of bits in n. Instead of appending the values you get to your list, set the value in the list at length-i-1 to the result of your AND.
Extra Tasks
These are meant to be even more challenging than the previous ones. Stick with using bitwise operations to do these rather than looking for solutions by cheekily converting your numbers to strings.
- Turn off the rightmost set bit (not necessarily bit 0). You should be able to do this without using a FOR loop or any if statements.
- Swap the nibbles of a byte. You should be able to do this with a single expression. Use a function that accepts a byte as a parameter. Don't use any arithmetic operators.
- Rotate the bits of a byte to the right (bits falling off the right edge should reappear on the left). Again, a single expression will suffice but it will be quite involved.
- Work out how to rotate bits to the left.
- Count the ON bits in an integer.
- Check if a binary pattern is palindromic.

