Python For GCSE
Mastermind
Introduction
The idea for this project is to make our own Python version of the classic two-player game, Mastermind.

In the classic game, one player chooses four coloured pegs and places them on their side of the board. The other player places coloured pegs on the opposite side, attempting to guess the pattern. The 'setter' then provides some feedback to the player. They use a white peg for each colour that is correct and in the correct place. They use a black peg for each correct colour that is not in the correct place. These feedback pegs do not let the player know exactly which of their guesses is correct, just the number.
The computer will generate a random 4 digit number using digits 0-9. The player makes a guess at the number. If the player does not guess the correct number, the computer gives feedback on the number of digits that are correct and correctly placed.
In this example, the computer number is 1234. The user guesses 1314. They have 2 correctly placed digits, the first and last ones. They have one digit (3) which is correct but in the wrong place.
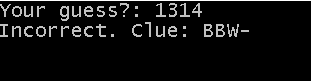
B means a black peg. In the Mastermind game, this is used to indicate a correct digit. It does not specify the position of that correct digit. W is a white peg. In the board game, this is a correct digit in an incorrect position. Dashes are used to pad out the feedback to 4 digits.
Data Structures
The easiest way for a user to enter a guess is going to be by typing in the 4 digits together. The computer pattern and each user guess will therefore be stored as integers. For example,
game_pattern = 1234
guess = 1314
These lines define the pattern and guess in the screenshot you saw earlier.
Numbers To Digits
In order to work with the digits, we’re going to need a way to convert numbers into arrays of their digits. Here’s a function to do this,
def num2digits(n):
ns = (4 - len(str(n))) * '0' + str(n)
return [int(d) for d in ns]
These two lines of code are doing a fair amount. The first line makes a string out of the number and, if the number does not have 4 digits, puts some 0s at the start.
The second line returns a list made from the characters in the string, working from left to right. This technique is called a list comprehension. It is a convenient way to set up a list when the values need something predictable done to them – in this case, converted back to an integer.
This function needs testing. Write a test procedure to do this – add some more suitable test values to the procedure below and change the italicised text into Python code.
def numtest():
test_values = [1234,2,23,0230]
for v in test_values:
print v and the the result of passing v to the num2digits function
Run the numtest procedure in the Shell and make sure that you are getting the results that you expect.
Giving Feedback
When we check the guess against the computer-generated pattern, we will be working out how many black and white pegs to use. It would make life easier for us if we wrote a function now that could convert those two numbers into the pattern we want. Here is the outline.

- Start by adding the string "B" to the variable s exactly b times. Use a FOR loop.
- Then add the string "W" to the variable eactly w times using another FOR loop.
- Design your own test code for your function. Add your function, test code and a few screenshots to your answer document.
Checking The Guess

This is the genuinely difficult part of this problem. Stick with me, little one, and all will be clear. To get the correct feedback, we must look at each digit of the guess and compare it to the pattern. If it matches, we add 1 to the black peg counter. If it does not match, we see if there is another digit in the pattern that matches this one. If that is not a matching digit, we add 1 to white, for a correct digit in the wrong place. This is still pretty tricky. Here is the pseudocode you need for the red splodge, based on variables in the starter code.
IF guess[i] == pattern[i] THEN
Add one to b
ELSE
FOR otherdigit=0 To 3
IF guess[i] == pattern[otherdigit] THEN
IF guess[otherdigit] NOT EQUAL TO pattern[otherdigit] THEN
IF used[otherdigit] == FALSE THEN
Add one to w
Used[otherdigit]=TRUE
Break
END IF
END IF
END IF
END FOR
END IF
Convert this code to Python.
A quick test in the Shell, would be a line like this,

The first number, 1234, is the guess. The second number 1122 is the pattern you are trying to guess. The first digit is correct and correctly placed (B---). The second digit is incorrect and incorrectly placed (B---). The third digit is a correct digit and but it is in the wrong position (BW--). The last digit is a correct digit. Since the second digit has already been used for a white peg, the pattern stays the same (BW--).
The Game
Now you have the functions, you are ready to start programming the main game loop. You can do this in a procedure called play_game().
- At the very top of your code page, not inside your new procedure, import the random module.
- Start by generating a random integer for the pattern (0,9999).
- Set up a counter for the game. The number of guesses taken is the player’s score.
- Set a variable to store the player’s current guess. Set it to -1 to start with.
- The next part needs to repeat while the player’s current guess is not equal to the pattern.
- Ask the user to enter their guess.
- Increase the guess counter by 1.
- Check the guess against the feedback.
- If the feedback is “BBBB”, tell them they have guessed the pattern, otherwise, display the feedback.
Extension – Variations
Make the maximum digit variable in a menu at the start of the game. When the player chooses 5, then no digits above 5 should be used in the game. This would be mathematically equivalent to the actual game of MasterMind.
Extensions – Computer Player
In the game of Mastermind, players normally take turns at being the code cracker. You could program an AI player in several ways but it would be nice to make use of the CheckGuess function to get the computer to do something that a player couldn’t.
Before you make any guesses, there are 10000 possible solutions. Once you get the feedback from the first guess a large proportion of those possibilities can be eliminated.
Imagine you guessed 1234 at the pattern 1122. This gets the feedback BW--. Test all of your possible guesses against the guess you just made, using your CheckGuess function. Eliminate all of those guesses that don’t give the exact same feedback you got when tested against the pattern. Your next guess needs to come from this much smaller pool.
There is an optimal way to choose the next guess but random works well enough, since the feedback always reduces the number of possible guesses until you have only one left or randomly choose correctly.
This is quite a challenge to implement. The general idea is,
currentGuess = 1122
WHILE NOT solved
Result = GET FEEDBACK FROM OPPONENT
IF Result == "BBBB" THEN
Solved = TRUE
ELSE
Solved = FALSE
Filter possible guesses according to feedback
currentgues=randomly chosen item from possible guesses
END IF
END WHILE

