• Home
• Programming
• Computer Science
• Twisting Puzzles
• Arduino
• BBC micro:bit
• Raspberry Pi Pico

Python For GCSE

• Programming Section Home
• Python For GCSE Home

A: Starting Off

• Arithmetic Operators
• Variables & Assignment
• Casting
• User Input
• Output Statements
• Random Numbers
• Math Module
• Section A Exercises

B: Selection

• Comparison Operators
• If Statements
• Section B Exercises

C: Iteration

• For Loops
• While Loops
• Sequences With Python
• Practising For Loops
• Section C Exercises

D: Lists

• Lists In Python
• Lists Of Lists
• List Comprehensions
• Section D Exercises

E: String Handling

• Handling Strings
• Slicing Strings & Lists
• Section E Exercises

F: Subroutines

• Procedures
• Functions
• Quadratic Equations
• Section F Exercises

G: File Handling

• File Handling
• Making A Simple Database
• Section G Exercises

H: Turtle Graphics

• Moving & Drawing
• Controlling The Pen
• Some Examples

I: Bonus Material

• Validation
• Searching Algorithms
• Sorting Algorithms
• ASCII Art Sprites
• Mastermind
• Integer Sequences
• Bitwise Operators
• Adventures In Wordle
• Quiz Engine
• High Score Table
• Playing Cards
• Extra Tasks

 

Python For GCSE
Playing Cards

Introduction

In these tasks we are looking at how to write a program that works with a deck of cards.

Our cards will be represented by a number from 0 to 51.

The first 13 cards will be the clubs from Ace to King. Then we have diamonds, hearts and then spades.

This is the sorted deck and, because we know the number of the position of each card in the sorted deck, there are some ways we can work with these numbers to find out about a specific card.

The tasks here are mainly to write some functions. Each function will need to be tested to make sure that it works. Do all of your tasks in a single program. As you move through these tasks, you will get nearer to the point where you can make something approaching a game. You can add your test lines to the program and then remove them or you can use the shell to test your program as many of you did with the subroutines.

In the example section, you have some code to start you off. The first 4 lines define lists. These are needed in the program and need to come first. The variable deck is a list of the numbers for each card. The cards are numbered as mentioned above – 0 to 51.

The list suits, is a list containing the strings that are used for each card suit.

The list ranks is a list of the names of the cards going from Ace to King.

The list r is a short version of this for when we need a compact representation of the card name.

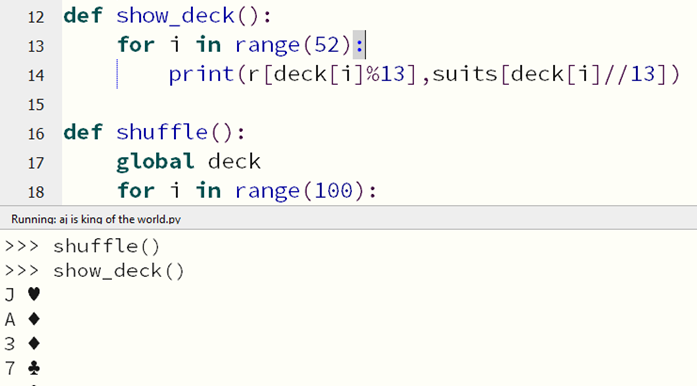
Example

deck = [i for i in range(52)]
suits = list("♣♦♥♠")
ranks = ["Ace","Two","Three","Four","Five","Six","Seven","Eight","Nine","Ten","Jack","Queen","King"]
r = ["A","2","3","4","5","6","7","8","9","10","J","Q","K"]


def display_sorted_deck():
    for i in range(52):
        print(r[i%13],suits[i//13])

Task 0. Get started

You need to start by making a program including the 4 lines from the example section. You can call display_sorted_deck() from the shell to see the list of cards.

Task 1. Shuffle()

This is done by choosing two random numbers and swapping the cards at those positions. Do this a lot of times. 50-100 is probably enough. So...(pseudocode)

FOR x = 0 to 99
    A = random number 0 to 51
    B = random number 0 to 51
    Tmp = deck[a]
    Deck[a] = deck[b]
    Deck[b] = tmp
END FOR

Task 2. Get_suit(c)

Floor divide c by 13 and return the value. You can do this by defining the function and then writing a single line with your return statement.

Task 3. Get_rank(c)

The rank is c modulus 13. Return the value.

Task 4. Get_card(c)

Use the other two functions (2 & 3) to help you to form a string of the card rank, followed by its suit. You are returning the string that you can make. Something similar to this is being done in the subroutine you were given at the start.

Task 5. Get_card_num(cardstring)

If the string is longer than 2 characters, the card has to be a 10. That's the only rank that needs two characters. If it is not longer than 2, the rank will be found from the first character in the string. cardstring[0] You can access the last character of a string by using the index -1 to find the suit. In both cases, the values you find need to be looked for in the lists. You are trying to find the index of the item. For example,

Rank = r.index("9")

You will be using a variable instead of a quoted literal.

Task 6. Deal(n)

In this subroutine, you are going to change the deck. To be able to do this, we need to write the following as the first line of the subroutine,

global deck

You need to take n cards from the list using a slice technique. You want to return a list of n cards, taken from the beginning of the deck. Don't forget that you also need to change the deck variable making it equal to the part of the list that wasn't spliced to make the hand. Here is a splodged outline for you,

Task 7. Display_hand(h)

This subroutine should take a list of integers that represent a hand. It should print the hand nicely for the user to see in the shell. You might start this by sorting the list. Then you convert each item in the list to its string representation. You could use a list comprehension to do this if you like. This might help.

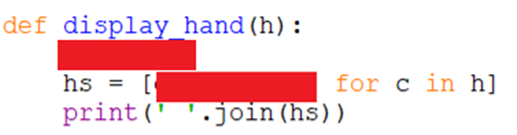
If you can desplodge the above, you have this done pretty neatly. The first line sorts the list (h). The second line makes a list of card strings. You need to use the get_card function to do this. The last line is done for you. It joins the list of card strings with a space between them. This makes it easier to test the previous function.

Reflection

This is an important time to stop for a brief moment to think about what you have done so far. The code you have is good enough to use as the basis for anything that you want to do with playing cards.

• None of what you have done so far has been explicitly connected to any card game. When you want to write complex programs, it is a good idea to work like this.
• We have a way of representing the deck by allocating an integer from 0-51 to each card. Each integer maps onto exactly one card. To play any sort of game, we need to be able to easily identify a card.
• We can shuffle that deck of cards. All card games begin with a shuffled deck.
• We can tell the rank or suit of a card from its number. In card games, having groups of cards of the same rank, same suit or in sequential order of rank makes a difference. We have the means now to be able to work these things out.
• We can 'deal' a number of cards from the top of the deck. This removes them from the deck. Card games work like this.
• We can represent a hand in a card game using a list of integers. We can display this list with the card names for the user.

Everything else that we want to do depends on what has been done so far. If we haven't worked out how to do all of these things, the rest of the exercise is too complex for us.

When working on larger programs, it is important to think about the 'critical path' when deciding which things to do first. If we were not able to shuffle the deck, there is no sense of a game. If we couldn't work out the suit or rank of a card, we couldn't display it properly, couldn't compare a player's hand with another. Each step is needed for the later steps to be possible and anything more ambitious like a game or a program to explore experimental probability in card games.

3 Card Brag (Poker)

3 Card Brag is a poker variant based on hands of 3 cards. When played as poker, the betting starts with players paying an ante (with or without blind antes). Betting usually continues until 2 players are left. There are no draw phases – the hand does not change.

Another version of the game is played with 2-4 players. 13 cards are dealt to each player. Each player makes up to 4 hands. Pairs are only allowed on the 4th hand and High Card hands do not count. This game is called Crash.

Hand Type Function

Score	Rank	Description	Frequency	Probability
5	Prial	Three cards of same rank	48	0.22%
4	Straight flush	Three suited cards in sequence	48	0.22%
3	Straight	Three cards in sequence	720	3.26%
2	Flush	Three suited cards	1,096	4.96%
1	Pair	Two cards of same rank	3,744	16.94%
0	High card	None of the above	16,440	74.39%

The highest scoring hand types are at the top of the table. When comparing two hands, we first check the type of hand. A prial beats a straight flush, beats a straight and so on. If the two hand types are different, it's easy to pick a winner.

This function is complex (consists of many parts). None of those parts are difficult to execute but you do need to concentrate and check your work as you go. Start off with this code,

def hand_type(hand):
    # make a list of the ranks 
    rs = [get_rank(i) for i in hand]
    # make a list of the suits
    ss = [get_suit(i) for i in hand]
    # Prial
    if rs[0] == rs[1] and rs[2] == rs[1]:
        return 5
    # All same suit (flush)

    # Sequential ranks or AKQ (straight)

    # Straight Flush

    # Straight

    # Flush

    # pair - ranks are sorted

    # None of the above - must be high card
    return 0

Step 1 – Copy And Paste Prial

Copy and paste the function from above. The first two lines make list of the ranks and suits of the cards using the list comprehension technique. This makes it easier for us to check for each hand type.

The check for a prial has been done for you. If the 3 cards in the hand have the same rank, you have a prial, the highest scoring type of hand. We return a 5 if this is true.

The rest of the code is mainly comments. These are the jobs we have to do and the order in which we write and test the code.

The way to test this is to write your own hand in the Shell and see if the function returns the value that you expect.

You'll need to do something like this, with more than just one hand, each time you work out the code for a different hand type.

Step 2 – Work Out How To Test For A Flush & Straight

You need a fair bit of code to get to the point where you can test this. The first step here follows on from the previous and is similar. Think about what you do at each point and the next splodge gets easier to work out.

This needs extensive testing of each hand type just like the example for the previous step.

Step 3 – Pair

Checking for a pair is something you should now be able to do yourself. The list of ranks (rs) is the one you need to look at. If the first two items or the last two items in the list are the same, you have a pair. The list is sorted. This means that the first and last items cannot be the same (otherwise it would have been a prial). Test again.

Extension 1 – Breather

I wrote a list of the hand type names as a global variable. I wrote a demo subroutine that defines a deck, shuffles it, draws 3 cards at a time until the deck is exhausted, printing out the hand and type for each one. See if you can work out how I did this. In order to make the printing work nicely, I wrote a modified subroutine to create a string of a hand rather than print it.

Extension 2 Breather – Better Hand Display

If you look at the output on the previous page, the hands don't always display the way you would want. You could fix this with another subroutine.

The subroutine should accept the hand as a parameter and return a string representation that is optimised.

In the subroutine, find and store the hand type of the hand.

If the hand type is a prial (5) or straight flush (4), then it will be in the order you want.

For a straight, you want to get them in rank order, lowest to highest. If you have QKA though, it needs to have the ace last to make sense.

For a flush, you want the cards in rank order, highest to lowest.

For a pair, you want the pair to be the first two cards.

For a high card, you want the cards to be in rank order, highest to lowest.

This takes quite a lot of code to do. The result makes game play much nicer for the user, though. It is worth the effort.

Back To The Main Task – Comparing 2 Hands

This is the last major job you need to complete in order to make a playable game. We need a way to take two hands and work out which one is better.

Before we do this or go any further, it would be wise to work out some lists of integers to use as test values for your function. Get yourself 4 or 5 of each type ready to use quickly. You could define these in code if you want or simply type them up somewhere useful in the form you need.

The function should return,

• -1 if handa beats handb
• 1 if handb beats handa
• 0 if the hands are equal.

You can start by comparing the hand type for each hand. If they are different, you have a clear winner.

If the hand types are the same, you have more work to do...

A draw is possible with all hand types except Prial. There is a ranking system within each hand type. This can be summarised as follows. These lines are written as Python comments, you can copy and paste them to your program.

# Card rankings - these are for 3 card brag - highest to lowest
# 5 PRIAL                       333,AAA,KKK,QQQ,JJJ,101010,...
# 4 STRAIGHT FLUSH              A23,QKA,JQK,10JQ,... (SUITED)
# 3 STRAIGHT                    A23,QKA,JQK,10JQ,... (MIXED SUITS)
# 2 FLUSH                       AKJ,AK10,... (SAME SUIT - RANK OF HIGH CARD, SECOND CARD,..)
# 1 PAIR                        AAK,AAQ (RANK OF PAIR, RANK OF HIGH CARD)
# 0 HIGH CARD                   AKJ (MIXED SUITS)

Prials

When both hands are prials, you check the rank of a single card from each list. If one of them has 3s, they win, then aces, then by highest rank. (You can use the max function for that.)

Straight & Straight Flush

Check for [0,1,2]. Then check for [0,11,12]. Then look for the highest card in each list. Highest one wins. There can also be a draw here.

Flush

Find the highest ranking card of each flush. If these are the same, check the next highest. If these are the same, check the last one. There can be a draw here.

Pairs

Find the value of the pair. Check for aces. Then check by highest rank. If the ranks of the pairs are the same, the highest rank (or ace) of the other card wins, otherwise a draw.

High Card

Like the flush. Can also be a draw.

When you finish this function, you need a decent amount of testing before going any further. There has been a lot of intricate work and there must have been some ups and downs on the way. Look hard for any mistakes and make sure all of the programming logic is made to fire through your choice of test values.

Ways To Play

Choose your path wisely.

Mathematical Interest

Look again at the Extension task earlier. Expand on that principle to see how many deals it takes to get a prial. Work out the highest hand from each deal and only output that. Do hundreds of deals and record the results. Check the probabilities from the table above. Generate huge numbers of hands and see if experimental probability matches the table of theoretical probabilities.

Against The Computer – Full Deck

Rework the dealing so that you can make two lists of integers – a hand for the player and one for the computer. Make it so that cards are taken one at a time from the deck as though they were dealt. To play through the full deck, you need to use a while loop. The while loop should stop continue while the length of the deck list variable is greater than the number of cards you deal on each iteration.

More Interaction

To make the game more interesting, deal 5 cards. Work out a way for the user to choose which cards to discard. The ones they keep form the hand that they play against the computer.

Endless Play

If you want to be able to play endlessly, you can put the discarded hands on the 'bottom' of the deck. You can append them to the list. When they are dealt again later, there will be a slight change of the order of the cards but they will start to group together in higher scoring combinations.

More Interesting Game

Deal 13 cards to each player. The player chooses 3 cards that form a scoring hand (not high card). These are removed from the hand. The player continues to form hands until they cannot do so. They score a point for each hand that they form.

Harder

Take the last idea. In the game of Crash, you have to play your hands in order of their strength. To be able to get a computer to do this, you could write a subroutine that takes a list of integers representing cards and returns a list of 3 cards that make the highest scoring hand. If no hand type other than high card can be found, the function should return an empty list.

You could use such a function to make a computer player for Crash or even an automated card game program that plays the game for you. Deal two hands of 13 cards. These are automatically sorted into separate 3-card scoring hands and arranged in order from highest to lowest. For two players, the best hands are compared and the winning hand earns a point. Then the next highest hands are compared, and so on.

In the game of Crash, a pair can only be played as the 4th hand. You can only have a 4th hand if you have a first, second and third.

Creative

Find another way to play. Perhaps you play it like solo Yahtzee, with scores for the hands you can make from a particular amount of cards. Perhaps you work out a betting system against the computer. Your choice.