Introduction To Haskell
What Is A Function?
Introduction
From the specification,
- Know that a function, f, has a function type f: A → B (where the type is A → B, A is the argument type, and B is the result type).
- Know that A is called the domain and B is called the co-domain.
- Know that the domain and co-domain are always subsets of objects in some data type.
- A function is a rule that, for each element in A, assigns a value from B.
The domain is the set from which the function's input values or arguments are chosen.
The co-domain is the set from which the function's output values are chosen. Not all values from the set need to be outputs.
First Function
Write the following function definition in a text file and save it as square.hs,
squareOf x = x * x
This definition states that our function is to be called squareOf. Our function has one parameter. A parameter is a reference declared in a function definition.
Launch WinGHCI and load this file,
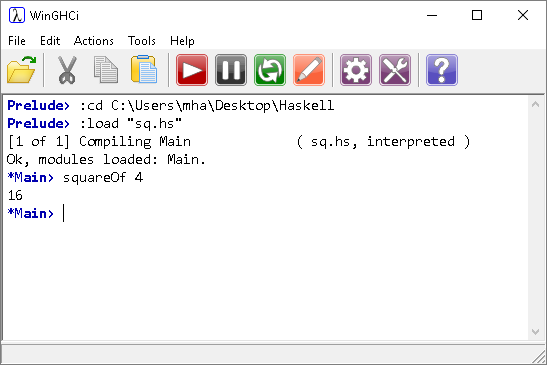
The line squareOf 4 is an example of function application. The term apply is used when we assign inputs to a function. Inputs to a function are called arguments. This distinguishes them conceptually from parameters, which exist only in the definition of a function.
Choosing Types
We can choose the types for our function by adding the following line to our program,
squareOf :: Integer -> Integer squareOf x = x * x
This extra line states that the function squareOf maps a big integer input onto a big integer output. It is called the type signature for the function.
We can check the types associated with our function in WinGHCi. This example shows the change that is made when we do that,
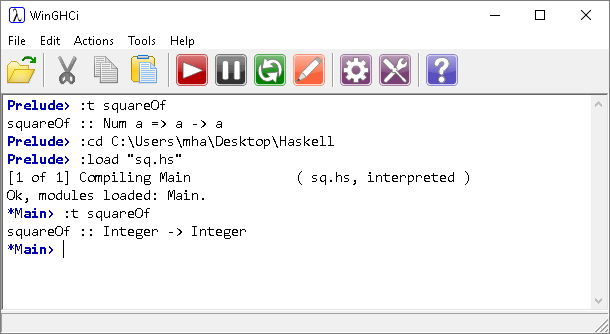
Numeric data types are inferred by Haskell. There are times when we want to force the compiler to choose a particular data type.
For example, when we calculate a factorial, we get a large number from relatively small inputs. We would get an overflow fairly quickly with standard integer sizes.
Here is the factorial program,
factorial :: Integer -> Integer factorial n = product [1..n]
The syntax of the language helps us to express this quite succinctly using a range to define our list and a function to calculate the product of that list.
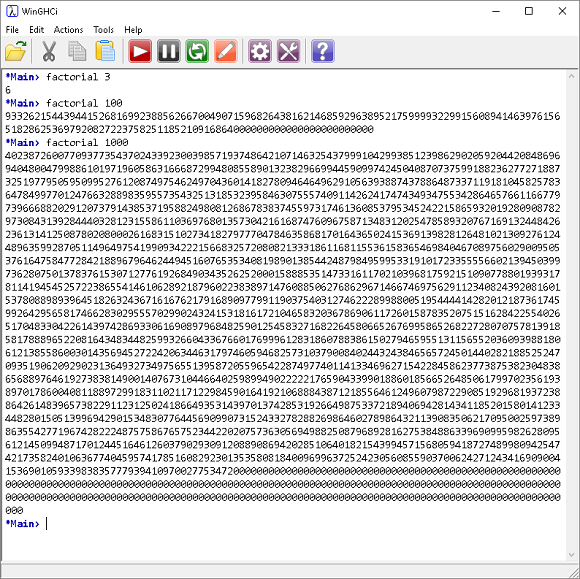
If you try a really large input and can't wait for it to finish executing, hit the pause button to interrupt the program and take back control.
More Function Application
Remember the definition from the specification,
f: A → B
This shows that the function f has a single parameter.
If we want to have our function accept more than one argument, we can do the following,
addTogether:: (Int, Int) -> Int addTogether (a, b) = a + b
In this case, we are defining our parameter as a tuple. Tuples are comma separated pairs of values contained in brackets. We can apply the function like so,
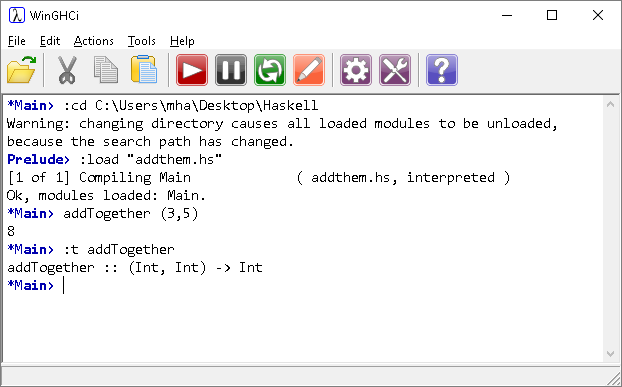
You could also write this function like this,
addThem a b = a + b
The notation required for the specification would have this described as,
addTogether: integer x integer → integer
You pronounce this, "Integer cross Integer maps to Integer".
Integer x Integer defines a Cartesian Product of the Integer set with itself. A x B means all of the ordered pairs of values from the sets A and B.
Imagine that our sets A and B each consisted of the integers 1 - 3. The Cartesian Product could be described using the following table.
| 1 | 2 | 3 | |
|---|---|---|---|
| 1 | (1,1) | (1,2) | (1,3) |
| 2 | (2,1) | (2,2) | (2,3) |
| 3 | (3,1) | (3,2) | (3,3) |

