Introduction To Haskell
Haskell Challenges
Introduction
This page has a selection of tasks that you could complete with Haskell. This is a selection of some of the simpler tasks that I worked on when learning Haskell and they are drawn from lots of sources.
Challenges
- Write a factorial function.
- Write a function to return the sum of the squares from 1 to n.
- Write functions for the nPr and nCr formulas.
- Write a function to determine if a number is prime. Use trial division.
- Determine whether a list is a palindrome. A palindromic list would be the same when reversed.
- Write a function to determine if a number is a square number.
- List the 5 digit numbers which are palindromic. There are several different ways to do this. Copy the toDigits function used in some of the examples. Remember that 5 digit numbers are in a predcitable numeric range and so don't need to be tested for by counting digits. Try this one using the filter function and then rerwrite it using a list comprehension.
- Write a function to solve quadratic equations. The function should determine whether or not the equation has real roots.
- Write functions to calculate the areas of shapes like triangles and quadrilaterals.
- Write a function to duplicate all of the elements in a list.
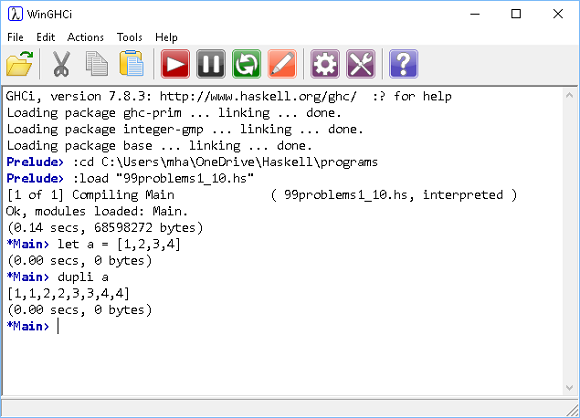
- Modify your duplicating function so that it can replicate items in a list a given number of times.
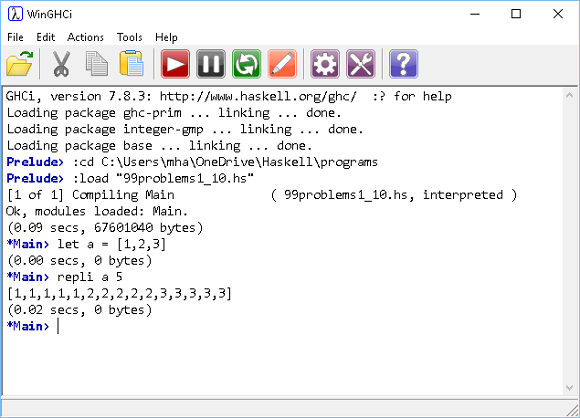
- Remove or drop every nth element from a list.
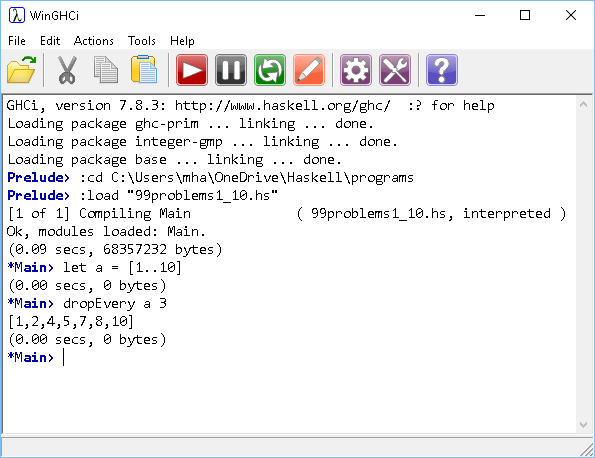
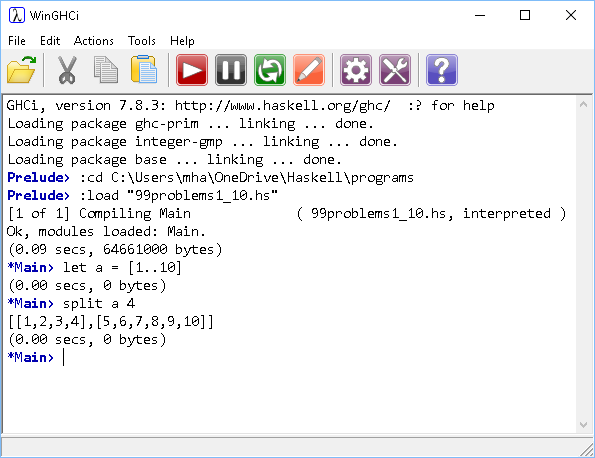
- Write a function to split a list into a list of a two lists at a given point.
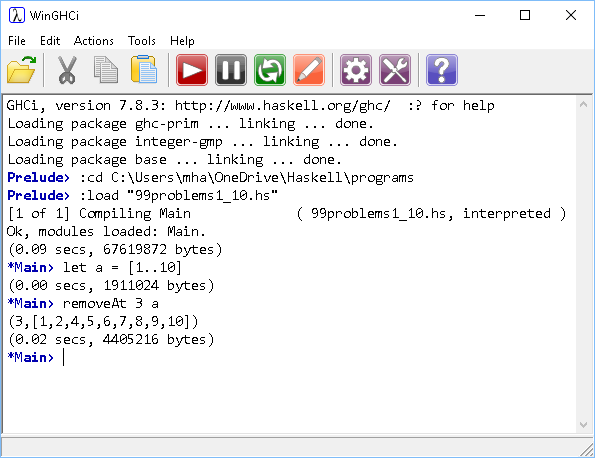
- Remove the nth element from a list. Return a tuple consisting of the removed item and the list that remains.
- Write a function that takes a list and returns the unique elements in that list.
- Write a program that makes an infinite list of abundant numbers. Abundant numbers are smaller than the sum of their proper divisors.
- Write a program that makes an infinite list of deficient numbers. Deficient numbers are larger than the sum of their proper divisors.
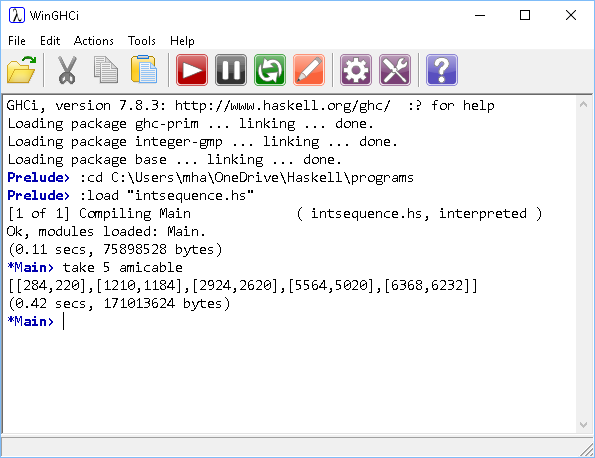
- Two integers a and b are said to be amicable numbers if the sum of the proper divisors of a is equal to b and the sum of the proper divisors of b is equal to a. Write a program to produce an infinite list of amicable numbers.
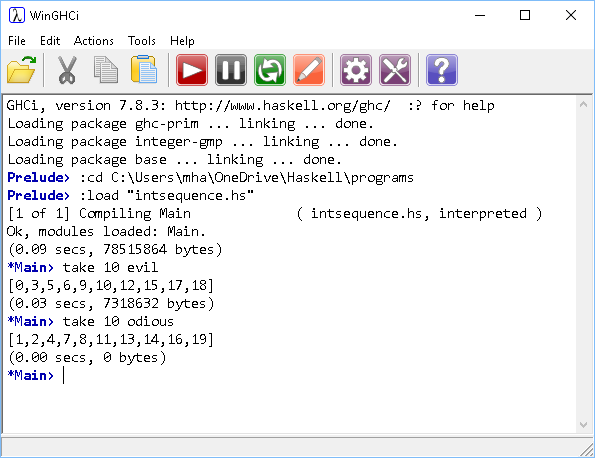
- An evil number is a non-negative integer that has an even number of 1s when represented in binary. An odious number has an odd number of 1s in its binary representation. Write two independently defined functions to produce infinite lists of evil and odious numbers.
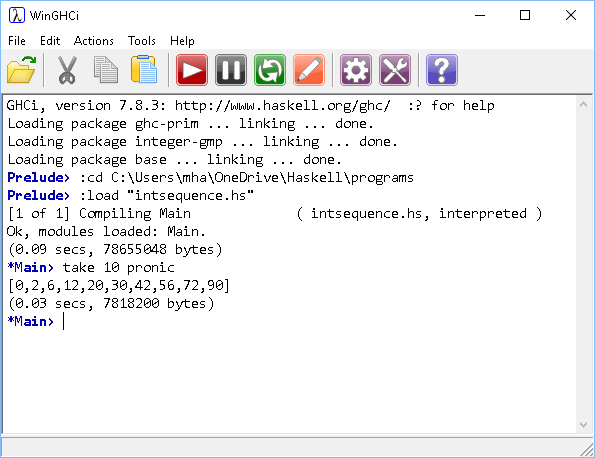
- Pronic numbers are integers which are the product of two consecutive integers. Write a function to produce an infinite list of pronic numbers.
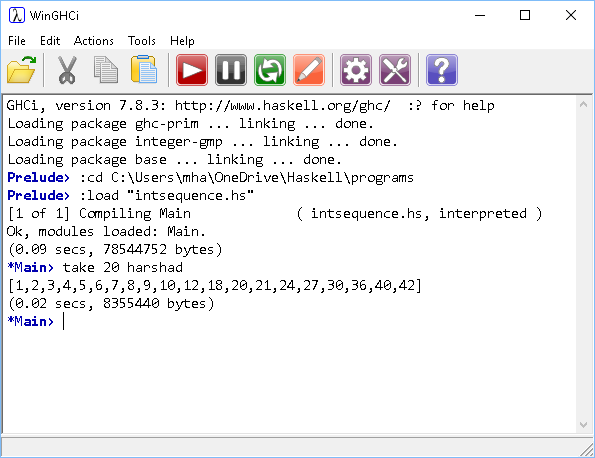
- Harshad numbers are integers which are divisible by the sum of their digits when written in a particular base. Write code to produce an infinite list of base 10 Harshad numbers.
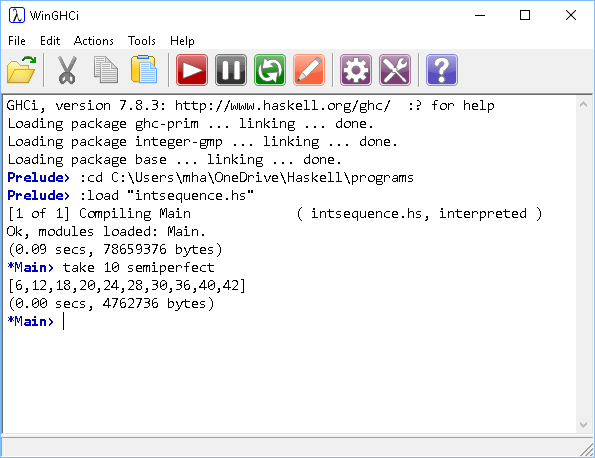
- Semi-perfect numbers are integers which are equal to the sum of all or some of its proper divisors. Have a look at the example with practical numbers for a way into this problem. Write code to produce an infinite list of semi-perfect numbers.
- Write a function that converts an integer from base 10 to any number base from 2 to 10.
- Determine all three-digit numbers N having the property that N is divisible by 11, and N/11 is equal to the sum of the squares of the digits of N. This was the first of three challenges in the 1960 International Mathematical Olympiad.
- Look up the various methods for determining the week day for a given date. You should be able to find several methods. Convert as many as you can into Haskell functions.
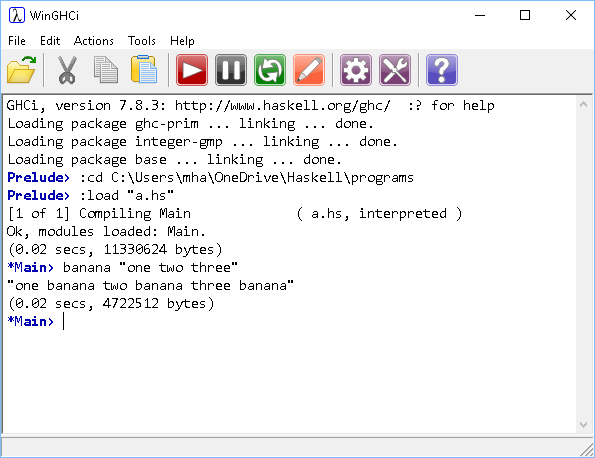
- Write a function that accepts a string and returns that string with the word 'banana' inserted between all of the words of the given string.
- Write a function to convert an integer into words. Choose the range of numbers you are prepared to work with.