Visual Basic 2010 (Console) Guide
Recursive Procedures & Functions
A procedure is recursive if the procedure contains a call to itself. This is perfectly legitimate in Visual Basic and most other high-level languages. A characteristic of recursive procedures is that there must be a stopping condition that can always be reached by the procedure regardless of the input.
The following procedure will calculate the factorial of a number (3! = 3 x 2 x 1 = 6) using a recursive technique.
Function RecursiveFactorial(ByVal f As Integer) As Integer
If f = 1 Then
Return 1
Else
Return f * RecursiveFactorial(f - 1)
End If
End Function
Sub Main()
Console.WriteLine(RecursiveFactorial(5))
Console.ReadLine()
End Sub
The function works quite logically. The factorial of a number is the number multiplied by the factorial of the number minus 1. ( 3! = 3 x 2! )
The alternative to recursion is iteration. The factorial function can be re-written using an iterative approach.
Function IterativeFactorial(ByVal f As Integer) As Integer
Dim total As Integer = 1
For count = 1 To f
total *= count
Next
Return total
End Function
In this example, there is little to choose between the two approaches. The recursive function works a little more like our brain does and is concise. The iterative function is a teeny bit longer but no harder to understand.
Fibonacci Numbers - The Revenge Of Recursion
Fibonacci numbers are numbers in the following sequence,
0, 1, 1, 2, 3, 5, 8, ...
After 0 and 1, each number is the sum of the previous two numbers in the series. The following pseudocode functions illustrate the difference between a recursive and iterative solution.
Fibonacci - Recursive
function fib1(n)
if n = 0: return 0
if n = 1: return 1
return fib1(n - 1) + fib1(n - 2)
End Function
Fibonacci - Iterative
function fib2(n)
if n = 0: return 0
if n = 1: return 1
create an array f[0 … n]
f[0] = 0, f[1] = 1
for i = 2 … n:
f[i] = f[i -1] + f[i - 2]
return f[n]
End Function
On the face of it, you'd think that the recursive function would be better. There are fewer lines of code and they are very similar to the steps that we would follow as humans doing the same calculation. You'd be wrong though - there is a major difference between the two approaches.
In the recursive function, every time that a recursive call is made, the program branches to the new function call. Since the program was in the middle of executing another call to the same function, it needs to store the necessary information to allow it to return to the point where it branched. This information is stored in a data structure called a stack and is placed on the top of the stack. When the program has finished executing the new function, it returns to the stack, finds the values it was working with before and completes the unfinished function. In this function, there are lots of branches to place in the stack before returning and this slows the program down more than you might think.
The following program code contains VB implementations of the two functions described above. It uses the StopWatch class to time the execution of each algorithm.
Sub Main()
Dim numToFind As Integer
Console.Write("Enter the term you want to find ")
numToFind = Console.ReadLine()
Dim stopW As Stopwatch = New Stopwatch()
Dim term As Long
stopW.Reset()
stopW.Start()
term = IterativeFibonacci(numToFind)
stopW.Stop()
Console.WriteLine("Term no {0} = {1} Iterative: {2} Milliseconds", numToFind, term, stopW.ElapsedMilliseconds)
stopW.Reset()
stopW.Start()
term = RecursiveFibonacci(numToFind)
stopW.Stop()
Console.WriteLine("Term no {0} = {1} Recursive: {2} Milliseconds", numToFind, term, stopW.ElapsedMilliseconds)
Console.ReadLine()
End Sub
Function RecursiveFibonacci(ByVal a As Integer) As Long
If a = 0 Then Return 0
If a = 1 Then Return 1
Return RecursiveFibonacci(a - 1) + RecursiveFibonacci(a - 2)
End Function
Function IterativeFibonacci(ByVal a As Integer) As Long
If a = 0 Then Return 0
If a = 1 Then Return 1
Dim fibNums(a + 1) As Long
fibNums(0) = 0
fibNums(1) = 1
For count = 2 To a
fibNums(count) = fibNums(count - 1) + fibNums(count - 2)
Next
Return fibNums(a)
End Function
Copy and compile this program. Enter small numbers like 10 or 20 and you won't see a great deal of difference between the two functions. Crank things up to 50 or so and then you'll start to notice that there is a large difference between these two approaches. The problem is the number of function calls that are required by the recursive program. The following tree diagram shows the function calls for the 5th term of the sequence.
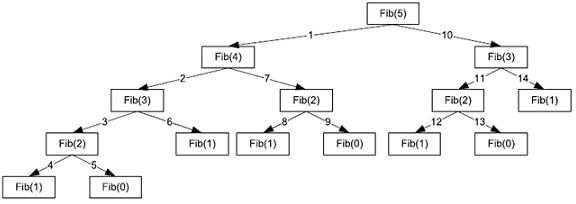
As n increases, the number of function calls quickly gets out of hand. If you look at the following table, you can see that by around n=10, the number of function calls is already very high. By n=20, the number of function calls is over 20000.
| n | Recursive Calls |
|---|---|
| 2 | 2 |
| 3 | 4 |
| 4 | 8 |
| 5 | 14 |
| 6 | 24 |
| 7 | 40 |
| 8 | 66 |
| 9 | 108 |
| 10 | 176 |
Each function call requires at least one line of code to be executed, maybe more. Each time n increases, the recursive procedure requires lots more lines of code. The iterative procedure increases by 1 loop iteration as n increases.

