Visual Basic 2010 (Console) Guide
Pocket Cube - Solving
Introduction
Nearly there. Our program has now calculated all of the information required to find solutions to any of the states that the puzzle can be scrambled into.
The solving procedure works as follows,
- Look up the current position in the table to get the distance
- Try out each of the possible moves
- If the move takes us to a position that is closer to solved, try out all moves from this new position
- Keep going until a solution is found
The only extra thing that we are going to do is to avoid making consecutive turns of the same axis. If turn a face clockwise and then turn the same face anticockwise, we have wasted two moves.
' Solving Procedure
Sub SolveAll(ByVal p As Integer, ByVal o As Integer, ByVal depth As Integer, ByVal solve As String, ByVal last As Integer)
If depth = 0 Then
'It's solved
Console.WriteLine(solve)
Else
For i As Integer = 0 To 8
If last \ 3 <> i \ 3 Then
If bigtable(perm(p, i), ori(o, i)) < depth Then
SolveAll(perm(p, i), ori(o, i), bigtable(perm(p, i), ori(o, i)), solve + " " + mvs(i), i)
End If
End If
Next
End If
End Sub
Notice that our procedure is recursive.
Testing The Procedure
Replace the Sub Main with the following version.
Sub Main()
CreatePermTables()
CreateOrientationTables()
CreateMonsterTable()
Dim pp() As Byte = {0, 2, 1, 3, 4, 5, 6, 7}
SolveAll(PermutationToIndex(pp, 7), 0, bigtable(PermutationToIndex(pp, 7), 0), "", -1)
Console.ReadLine()
End Sub
Notice that I have declared an array with the pieces 1 & 2 swapped around and assumed that all of the pieces are correclty oriented. Run the program and you get the following solutions at the end,
R2 F U' R U F2 R2 F R F'
R2 F U' R' F2 R2 U' F' R F'
R2 F2 R F R' F2 R U' R U
R2 F2 R' U' R F2 R' U R' U'
R2 F' R F R2 F2 U F U' F
R2 F' R F' U' F2 R2 F' U' F
R2 U F U' R F2 R' F R F2
R2 U' F' R F' R2 F U' R' F2
U F2 R2 F U F' R2 F U' F
U R U' R F2 R' U R F2 R2
U' F2 R2 F' U' F R2 F' R F'
U' R' U R' F2 R F' R' F2 R2
Test these sequences out on a pocket cube and you will find that they swap the two top right corners around. All of these sequence do that in optimal time. You might notice that some of the moves begin with U turns. If you do these moves without the U turn at the start you will still swap two pieces around, just not the two you expected. Change the way you recognise the situation and you'll have a move sequence one move shorter than you expected.
For a real test, you need to scramble the cube up good and proper. Choose one piece to be your back bottom left corner and then look at the remaining pieces. The permutations are quite easy to describe. Orientation is a little more fiddly though. The following tips might help,
If the sticker on the top and bottom faces is the colour of either of those faces, the piece has orientation 0.
For pieces in top layer positions the following diagrams show the positions of top layer stickers for clockwise (1) and anticlockwise positions (2).
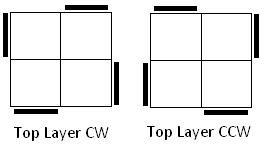
For pieces in bottom layer positions, the opposite of what you see in the image is true. The left hand diagram shows the anticlockwise positions and the right hand one the clockwise.
When you have worked out the orientations, check that the total is a number which divides exactly by 3. If not, check again, you will have got at least one wrong.

