Visual C# Guide
Floppy Cube Project - God's Algorithm
God's Algorithm
In cubing, the term, God's Algorithm is used to refer to a method of solving a puzzle using the shortest possible sequence of moves for any given position. In practical terms, we are looking for a table of unique positions and the sequences of moves (or algorithms) that generate them. Each entry is the optimal (shortest) method of generating that state. When the number of positions for a puzzle is relatively small, it is easy to perform the calculation on a computer. Fortunately, the floppy cube is one such puzzle.
Data Representation
Our solution is not based on having a computer turn an actual puzzle and then look at it to say what state it is in. We are looking to represent the puzzle in an abstract way. This means storing key information about the puzzle.
Representing Cube States
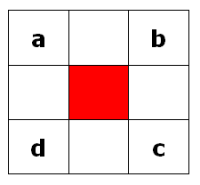
We can represent the positions of the corners using the letters a-d as shown in the diagram above.
The edges don't move, but we need to keep track of their orientations. We can use a 0 to represent a correctly oriented edge and a 1 to represent the incorrectly flipped edges.
A string of the corner positions followed by a string of edge states ab, bc, cd, da would give us a solved puzzle string of,
abcd0000
As a global variable this would be,
// solved positions
private static string solvedPosition = "abcd0000";
Turns
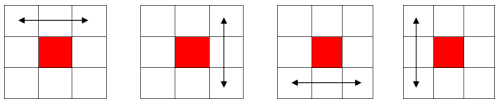
The diagram shows the possible turns on the floppy cube. We can represent each turn with the numbers 0 to 3 in the same order as the diagram. A sequence of turns can be stored as a string of these characters.
The effect of each turn would be to reorder the string of positions and edge states from above. Using our solved corner position (abcd) as a reference, the position of each corner after each of the 4 turns can be represented with the following table,
| Turn | a | b | c | d |
|---|---|---|---|---|
| 0 | 1 | 0 | 2 | 3 |
| 1 | 0 | 2 | 1 | 3 |
| 2 | 0 | 3 | 1 | 2 |
| 3 | 3 | 1 | 2 | 0 |
Meaning that, when you do turn 0, the piece at position 1 goes to position 0, 1 to 0. 2 and 3 stay where they were. This can be a 2d integer array as follows,
// transition table for position changes
private static int[,] mapPositions = { { 1, 0, 2, 3 }, { 0, 2, 1, 3 },
{ 0, 1, 3, 2 }, { 3, 1, 2, 0 } };
Move Table
Each time we find a new position, we need to store it. We can use a Dictionary to do that. We can use the generic List structure to store all of the unique postions ar each depth. We'll assume no more than 14 turns to start with - we can adjust this number up or down when we have executed the program.
// dictionary to store moves
private static Dictionary<string,string> moveTable = new Dictionary<string,string>();
// list to store moves at each depth
private static List<string>[] positionsAtDepth = new List<string>[15];

