Ciphers
Substitution Ciphers
Transposition Ciphers
Polybius Square
Steganography
Trifid Cipher
Introduction
The Trifid cipher is a person-killing plant-creature from space another of Félix Delastelle's ciphers. It extends the concept behind the Bifd cipher to a third dimension.
Normal, the squares are filled in a less predictable way. To simplify the process, we'll use them as you see in the diagram below,
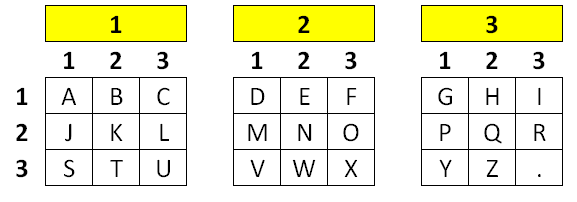
In essence, we have 3 ickle Polybius squares. We'll call each square a table. There are three rows and three columns on each table. Each of these three pieces of information forms a set of co-ordinates in 3 dimensional space. We'll use the following order for our representation of these co-ordinates,
(table, row, column)
This makes the co-ordinates of each character,
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | . | |
| Table | 1 | 1 | 1 | 2 | 2 | 2 | 3 | 3 | 3 | 1 | 1 | 1 | 2 | 2 | 2 | 3 | 3 | 3 | 1 | 1 | 1 | 2 | 2 | 2 | 3 | 3 | 3 |
| Row | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| Column | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 1 | 1 | 2 | 3 | 1 | 2 | 3 |
Now let's encipher a message. Our message is, 'The secret is out.'. We'll remove the spaces and turn everything into upper case. So the mesage is 'THESECRETISOUT.'. Next we write out the message with the table, row and column numbers written below,
| T | H | E | S | E | C | R | E | T | I | S | O | U | T | . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 2 | 1 | 2 | 1 | 3 | 2 | 1 | 3 | 1 | 2 | 3 | 1 | 3 |
| 3 | 1 | 1 | 3 | 1 | 1 | 2 | 1 | 3 | 1 | 3 | 2 | 3 | 3 | 3 |
| 2 | 2 | 2 | 1 | 2 | 3 | 3 | 2 | 2 | 3 | 1 | 3 | 3 | 2 | 3 |
As with the Bifd cipher, we then read off co-ordinates from left to right and use the letters at these positions in our cipher text.
| 132 | 121 | 321 | 312 | 113 | 311 | 311 | 213 | 132 | 333 | 222 | 123 | 322 | 313 | 323 |
| T | J | P | H | C | G | G | F | T | . | N | L | Q | I | R |
Programming The Cipher
As with the tap code and Bifid cipher, we can keep the cipher alphabet as a string. We just need to work out how to transform positions in the cipher alphabet into tables, rows and columns that we use for the co-ordinates.
To help us work this out, we can write out the table from above using numbers instead of letters,
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | |
| Table | 1 | 1 | 1 | 2 | 2 | 2 | 3 | 3 | 3 | 1 | 1 | 1 | 2 | 2 | 2 | 3 | 3 | 3 | 1 | 1 | 1 | 2 | 2 | 2 | 3 | 3 | 3 |
| Row | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| Column | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
We need to find ways to work out each of the 3 co-ordinates from just the position in the cipher alphabet. We also need to be able to work out the position from the co-ordinates.
- The table is calculated by doing (position MOD 9) DIV 3 + 1.
- The row is calculated by doing position DIV 9 + 1.
- The column is calculated by doing position MOD 3 + 1.
- The position is calculated by doing, 3t + c + 9r - 13 where the letters represent the table, column and row numbers.
These transformations allows us to build a cipher alphabet randomly and store it in a single string. We won't need to make our program search through a 3 dimensional array when we encrypt and decrypt.
Encryption
plain ← "THESECRETISOUT."
cipherAlphabet ← "ABCDEFGHIJKLMNOPQRSTUVWXYZ."
DECLARE INTEGER new_places[plain.LENGTH * 3 - 1]
FOR i ← 0 TO plain.LENGTH - 1
position ← cipherAlphabet.INDEXOF(plain(i))
new_places[i] = ((position Mod 9) \ 3) + 1
new_places[i + plain.Length] = (position \ 9) + 1
new_places[i + (plain.Length * 2)] = (position Mod 3) + 1
END FOR
cipher ← ""
counter ← 0
FOR i ← 0 TO plain.LENGTH - 1
cipher ← cipher + cipherAlphabet((new_places[counter] * 3) + new_places[counter + 2] + (new_places[counter + 1] * 9) - 13)
counter ← counter + 3
END FOR
OUTPUT cipher
Decryption
cipher ← "TJPHCGGFT.NLQIR"
cipherAlphabet ← "ABCDEFGHIJKLMNOPQRSTUVWXYZ."
DECLARE INTEGER new_places[cipher.LENGTH * 3 - 1]
FOR i ← 0 TO cipher.LENGTH - 1
position ← cipherAlphabet.INDEXOF(cipher(i))
new_places[counter] = ((position Mod 9) \ 3) + 1
new_places[counter + 1] = (position \ 9) + 1
new_places[counter + 2] = (position Mod 3) + 1
counter ← counter + 3
END FOR
plain ← ""
FOR i ← 0 TO plain.LENGTH - 1
plain ← plain + cipherAlphabet((new_places[i] * 3) + new_places[i + (cipher.LENGTH * 2)] + (new_places[i + cipher.LENGTH] * 9) - 13)
END FOR
OUTPUT plain