Twisting Puzzles
2-Layer Cheese - Solution
Introduction

The first thing to work out is what we mean by 'solved'. Look carefully at the picture. The top and bottom faces are separated into their respective colours and each of the edge pieces matches with the one on the opposite layer.
At this point, you may have some order for the colours that you want to get. I just stop when it looks done.
Notation
There are 3 turns used in the solution. They are numbered 0, 1 & 2. Turn over the section marked green in the following diagrams.
Turn 0
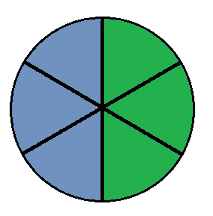
Turn 1
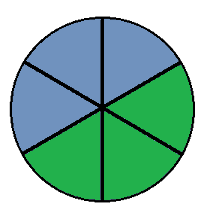
Turn 2
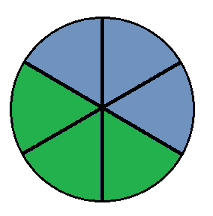
Other
The only other turn used is one of the bottom or d layer. This is shown in the algorithms in the form 3D, where the 3 means that you do 3 clockwise turns of the D layer.
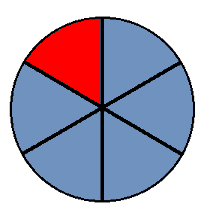
Fixed Point Of Reference
When performing sequences of moves, you need a fixed point of reference throughout. You can't rotate the whole puzzle in your hands and expect the algorithm to work. The fixed point of reference is the piece shown in the image below.
When doing turns 0 - 2, the red piece and its counterpart on the bottom layer are not affected.
Step 1 - Separate The Top & Bottom Layer Pieces By Colour
The first stage of the solution requires you to orient the pieces. This means making the top and bottom layer colours separate colours on each layer. You don't need any algorithms for this. Try to group the pieces into 3 of the same colour. When you get 5 of the same colour on each layer, you are 2 turns away from getting there.
When you are done, the top and bottom faces will be of one colour each but you won't be able to line up all of the edge pieces.
Step 2 - Match Up Edges
Rotate the layers with respect to one another until you have the most matches in the edge pieces.
In this step we move the pieces around on one of the layers so that they match the other. Start by deciding which layer's pieces you are going to rearrange and make that the top layer.
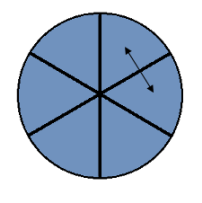 | 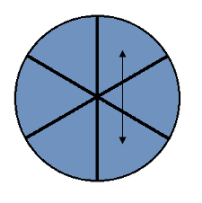 | 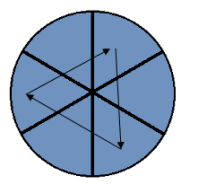 |
| 4D 0 2D 0 3D 2 0 1 1D 1 0 2 0 | 2D 1 0 2D 1 4D 0 2D 0 2D 1 0 | 0 2D 0 4D 2 0 4D 2 2D 2 |
The third algorithm, the shortest of the three, can be performed in reverse to cycle the other way.

